Andrew Valentine

Logo

Prior Sampling

How can you use machine learning to solve inverse problems? Prior sampling offers one solution: generate many candidate models (sampling from the prior); run a simulation for each to predict the corresponding observations; and then assimilate all this information using some kind of machine learning algorithm that can then be applied predictively to real data.

Contents

Back to research overview

Background

There is a long history of studies that have sought to apply machine learning to (geophysical) inverse problems. Early milestones include the works of Roth & Tarantola in 1994, and Devilee, Curtis & Roy Chowdhury in 1999. Then in 2007, Meier, Curtis & Trampert demonstrated geophysical inversion using a Mixture Density Network (MDN) – a framework proposed by Bishop where the outputs of a simple neural network are treated as the parameters for a Gaussian mixture model (GMM): in effect, the network outputs an entire probability density function.

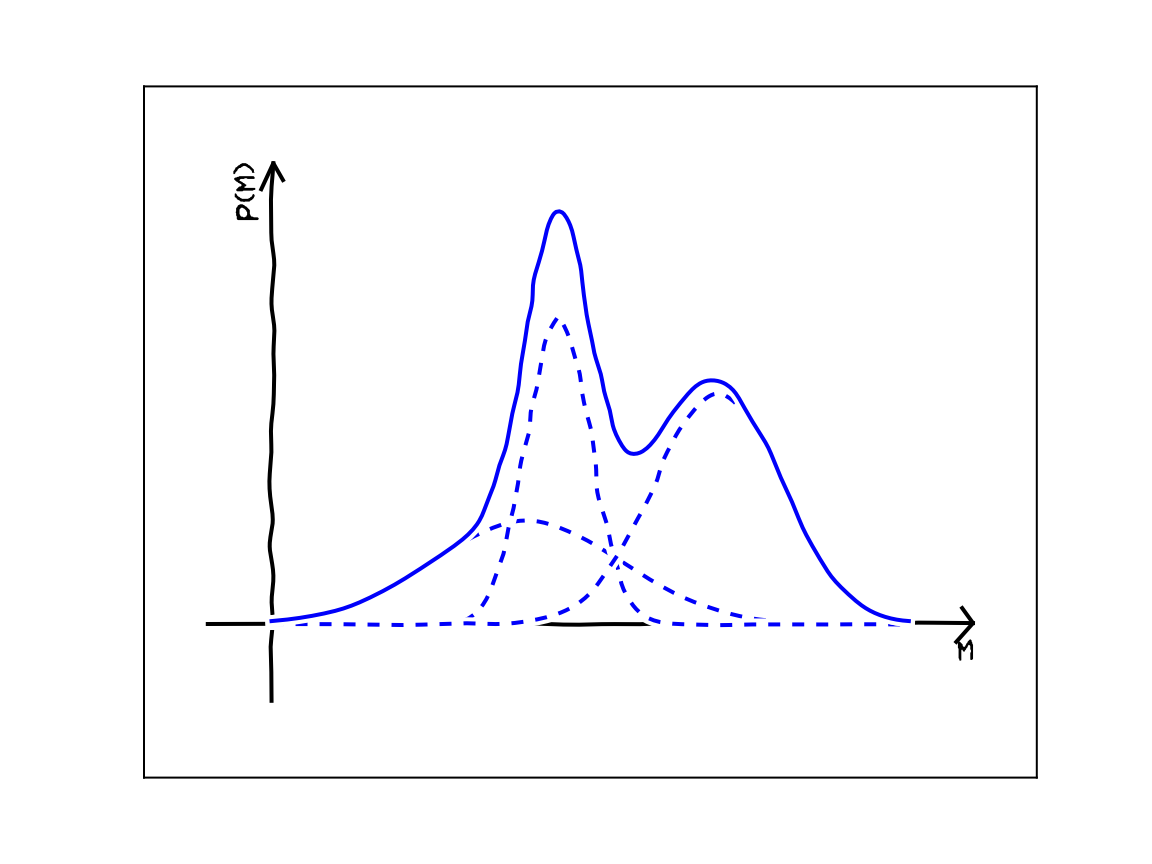
Gaussian Mixture Model

A three-component Gaussian mixture model.

In Meier et al.’s formulation, observed data are input to the neural network and an approximate posterior marginal distribution for each model parameter comes out. We picked up this work, exploring a number of different applications, and seeking to better-understand its theoretical basis. This is set out in detail in a paper written by Paul Käufl, which shows that the MDN-learned posteriors are exact in the limit of an exhaustive training set and infinite-capacity neural network.1

I wrote a Fortran(!) package implementating the MDN framework, which is available here.

Contents

Applications

We have applied the MDN approach to a variety of problems:

Earthquake early warning

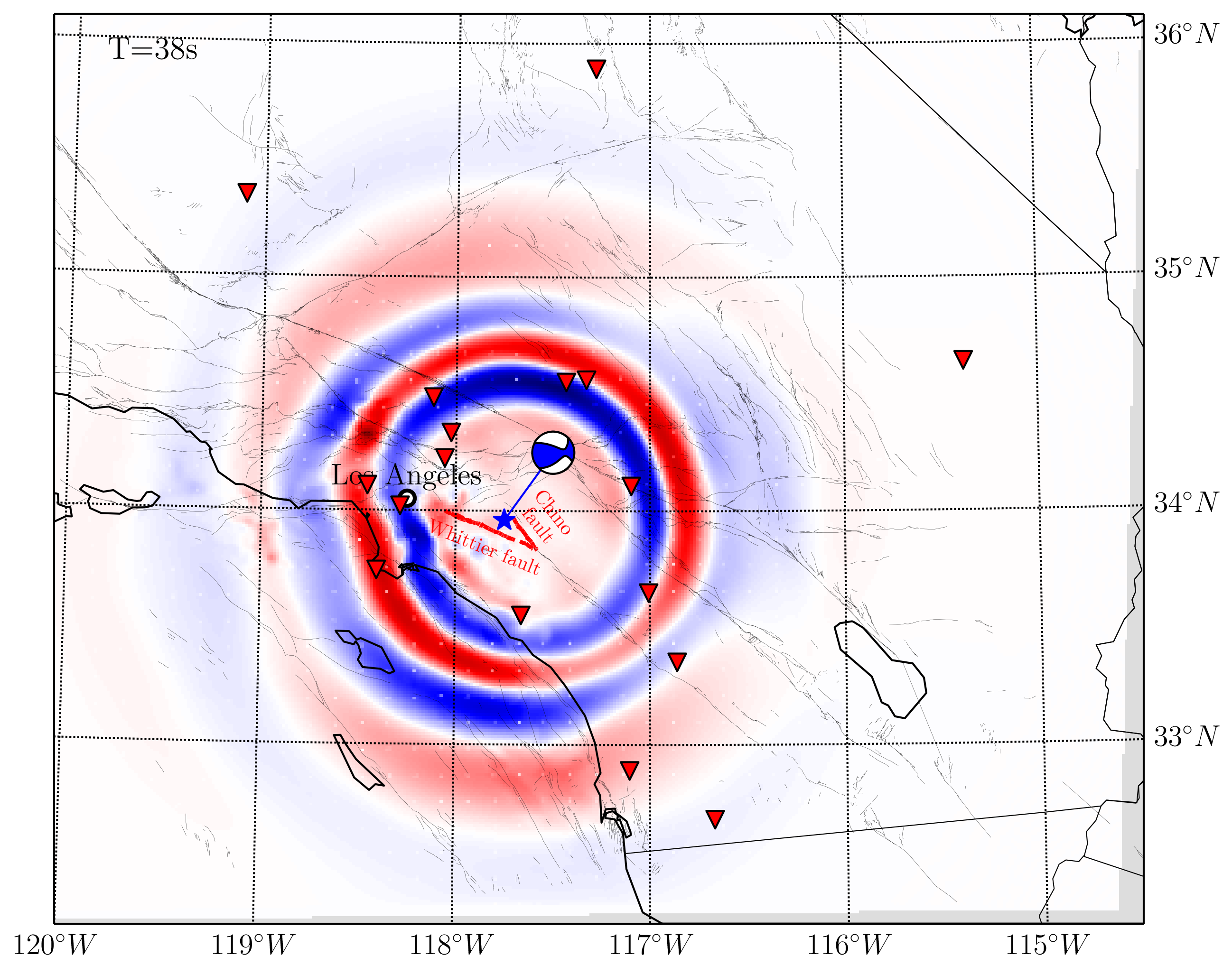
Chino Hills wavefield

Paul Käufl’s PhD thesis focussed on the potential of MDNs for rapid earthquake location and characterisation. We started with a comparatively simple class of data, and added complexity as we gained experience:

  1. Static displacement observations – two-component vectors at each site.2
  2. Simple waveforms within a 1D earth model.3
  3. Physically-complete waveforms using SPECFEM3D and a complex crustal model for Southern California.4

The last of these provides a convincing proof-of-concept for the feasibility of real-time earthquake early warning using physically-complete (computationally very expensive!) numerical modelling.

Earth’s radial seismic structure

Ralph de Wit’s PhD thesis focussed on a different seismological application: performing inference for the physical properties of the Earth as a function of depth. Again, we explored performance across different data sets:

  1. Travel times for body waves.5
  2. Eigenfrequencies for specific normal modes of the Earth.6

Global geodynamics

Suzanne Atkin’s PhD thesis looked at geodynamics, and whether MDNs could be used to infer thermochemical properties of the Earth from tomographic images. This is a challenging problem, with substantial computational difficulties, but we had some success.7

Mineral physics

Ashim Rijal has used the MDN framework to [model equations of state] for lower mantle minerals.8

Contents
Back to research overview

References

  1. Käufl, Valentine, de Wit & Trampert, 2016. Solving probabilistic inverse problems rapidly with prior samples. doi:10.1093/gji/ggw108 ↩

  2. Käufl, Valentine, O’Toole & Trampert, 2014. A framework for fast probabilistic centroid–moment-tensor determination — Inversion of regional static displacement measurements. doi:10.1093/gji/ggt473 ↩

  3. Käufl, Valentine, de Wit & Trampert, 2015. Robust and fast probabilistic source parameter estimation from near-field displacement waveforms using pattern recognition. doi:10.1785/0120150010 ↩

  4. Käufl, Valentine & Trampert, 2016. Probabilistic point source inversion of strong-motion data in 3D media using pattern recognition: A case study for the 2008 Mw5.4 Chino Hills earthquake. doi:10.1002/2016GL069887 ↩

  5. de Wit, Valentine & Trampert, 2014. Bayesian inference of Earth’s radial seismic structure from body wave travel times using neural networks. doi:10.1093/gji/ggt220 ↩

  6. de Wit, Käufl, Valentine & Trampert, 2015. Bayesian inversion of free oscillations for Earth’s radial (an)elastic structure. doi:10.1016/j.pepi.2014.09.004 ↩

  7. Atkins, Valentine, Tackley & Trampert, 2016. Using pattern recognition to infer parameters governing mantle convection. doi:10.1016/j.pepi.2016.05.016 ↩

  8. Rijal, Cobden, Trampert, Jackson & Valentine, 2021. Inferring material properties of the lower mantle minerals using mixture density networks. doi:10.1016/j.pepi.2021.106784 ↩